The Echo-nomist

When you hear the term “Game Theory”, what do you think? Is it about games? Well, yes and no. It is broader than the games people might play, like poker and chess. Game theory teaches us how to behave smartly in a given situation. It applies to countless exciting and thought-provoking aspects of decision-making in economics, business, politics, social interactions, and indeed to much of everyday life.

One of the most essential concepts of game theory is Prisoner’s dilemma. This concept gives us the basics of all the analysis required in decision making

Let’s take two people: Riya and Ram. They have both been arrested for drug dealing. Both of them have been taken to different cells to be interrogated, and the combination of their answers will determine their prison sentences. Ideally, the best solution (global optimum solution) for both of them is to not confess and spend only two years in jail, but the two don’t share a sense of loyalty and are hesitant to trust each other. So, the best decision for Riya would be to confess, as she would be better off regardless of what Ram says. This is Riya’s dominant strategy (best possible outcome no matter what the other person does). Similarly, Ram would also like to confess as he would be better off regardless of what Riya says.

Thus, both will end up confessing and spend 5 years in jail – that’s the game theory solution. This is the only outcome that has reached Nash equilibrium – a state in which the decision you take is better off no matter what the other person decides to do.

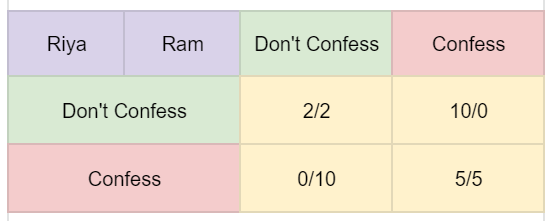
Here, both have found Nash equilibrium in grid 4. Even though the best solution would have been 2/2, this happens in competitive situations… no one can trust anybody.

Let’s take two people: Stan and Brandon. They own competing grocery stores next to each other. If Brandon prices his goods high, Stan’s best response would be to price his goods low as then he would earn 100$ more than if he prices high. Even if Brandon’s prices are low, his best response will still be to price low. So this is the dominant strategy of Stan.

Similarly, the dominant strategy of Brandon would be to price low as well. Hence, they both end up with the worst combined outcome while having Nash equilibrium. This is similar to price wars, where companies repeatedly cut down prices to provide the respective good for cheaper value. This is done to offer a competitive advantage over its competitors; however it just leads to lower and lower profit margins. This is exactly what happened between Coca cola and Pepsi a few years ago.

What will happen if people don’t understand game theory?

Let’s take a market which has two phone shops. If one vendor reduces his price, it will lead to the other reducing his price, and this will go on and on if the vendors don’t understand game theory. If the seller focuses on providing a differentiating factor instead of slashing prices, this may explain why the oligopoly market operates at fixed prices, and there is non-price competition.

Like the above examples, game theory can be applied anywhere, and its scope is unlimited. Game theory requires you to treat serious decision-making situations as a game, ironic, isn’t it? I would personally love to, but college admission season….. 

So, whenever we are in a difficult situation, let’s keep game theory in mind and try to make the best decision.